专为高中生提供有价值的资讯
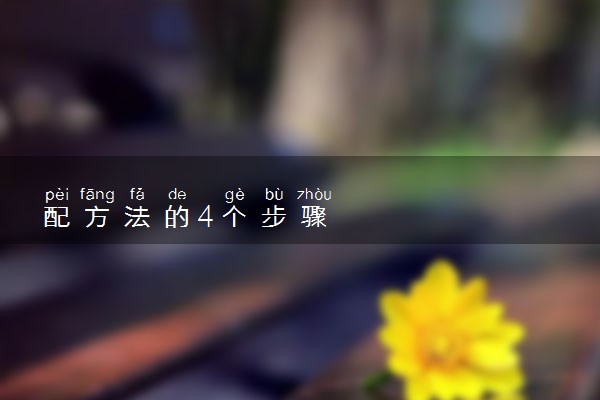
配方法是一种技巧,用于将二次多项式转变为一个一次多项式的平方与常数的和。它包含以下四个步骤:首先将原方程化为一般式,接着将系数调整为1,然后对方程两边进行平方处理,最后通过开平方来求解。
第一步:转化为一般式
首先,将原方程转化为一般形式,即aX²+bX+c=0(其中a≠0)。
第二步:调整系数为1
接着,将方程两边同时除以二次项系数,使得二次项系数为1,并将常数项移至方程右边。
第三步:方程两边平方处理
然后,将方程两边同时加上一次项系数一半的平方,使左边形成一个完全平方,右边则化为一个常数。
第四步:开平方求解
最后,通过直接开平方的方法求解方程。若右边为非负数,则方程有两个实根;若右边为负数,则方程有一对共轭虚根。
对于形如(X-m)²=n (n≥0)的一元二次方程,可以直接通过开平方的方法求得解为X=m±√n。
①等号左边为某数的平方,等号右边为常数。
②降次的本质是将一元二次方程转化为两个一元一次方程。
③具体方法是根据平方根的定义进行开平方。
Copyright 2019-2029 http://www.86gaokao.com 【八六高考】 皖ICP备19022700号-9
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告